Practice 3-2 proving lines parallel – In practice 3-2, we delve into the fascinating world of parallel lines, exploring their properties, methods of proof, and practical applications. From construction to architecture and engineering, the significance of parallel lines in our everyday lives is undeniable. This practice session empowers us to understand and demonstrate the parallelism of lines with precision and confidence.
Throughout this practice, we will investigate various techniques for proving lines parallel, including the slope method, intercept method, and angle relationships. We will also explore the concept of transversals and midsegments, which play a crucial role in establishing parallelism.
Identifying Parallel Lines
Parallel lines are a fundamental concept in geometry. They are defined as lines that never intersect, no matter how far they are extended. This property is known as the parallel postulate.
Parallel lines are often found in real-life situations. For example, the sides of a rectangle are parallel, as are the tracks of a railroad.
Properties of Parallel Lines
There are several important properties of parallel lines. First, the distance between two parallel lines is constant. This means that the lines will never get closer or farther apart as they are extended.
Second, the angles between two parallel lines and a transversal (a line that intersects both lines) are congruent. This means that the angles will have the same measure.
Third, the alternate interior angles of two parallel lines and a transversal are congruent. These are the angles that are on opposite sides of the transversal and inside the two parallel lines.
Fourth, the corresponding angles of two parallel lines and a transversal are congruent. These are the angles that are on the same side of the transversal and outside the two parallel lines.
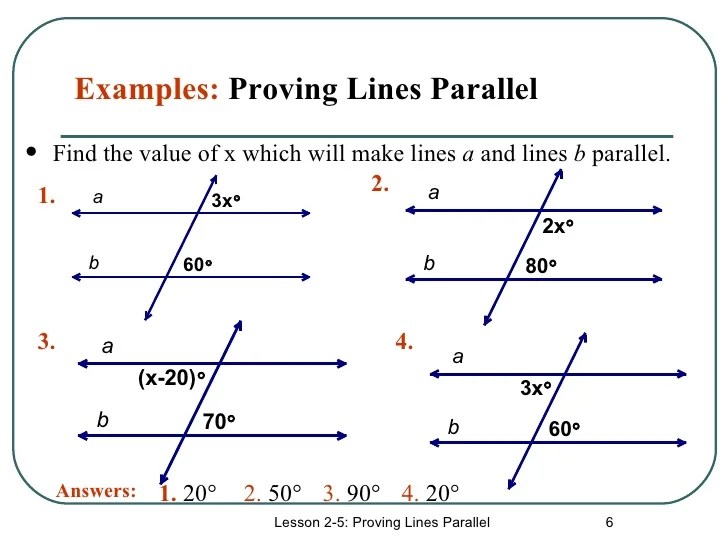
Methods of Proving Lines Parallel: Practice 3-2 Proving Lines Parallel
In geometry, proving lines parallel is a fundamental skill. Parallel lines are two lines that never intersect, no matter how far they are extended. There are several methods to prove lines parallel, including the slope method, the intercept method, and angle relationships.
Slope Method
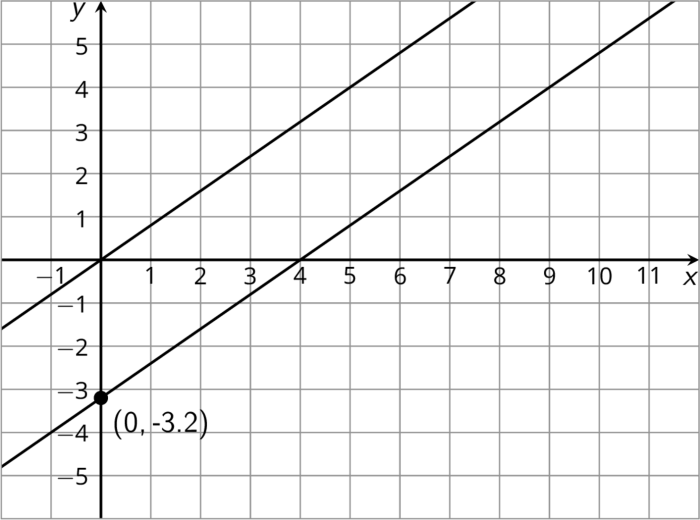
The slope method is a simple and effective way to prove lines parallel. The slope of a line is a measure of its steepness, and it is calculated by dividing the change in the y-coordinate by the change in the x-coordinate between any two points on the line.
If two lines have the same slope, then they are parallel.
To use the slope method to prove lines parallel, follow these steps:
- Find the slope of each line using the formula: slope = (y2
- y1) / (x2
- x1), where (x1, y1) and (x2, y2) are two points on the line.
- Compare the slopes of the two lines. If the slopes are equal, then the lines are parallel.
For example, consider the following two lines:
- Line 1: y = 2x + 1
- Line 2: y = 2x – 3
The slope of Line 1 is 2, and the slope of Line 2 is also 2. Therefore, the two lines are parallel.
Intercept Method
The intercept method is another simple method to prove lines parallel. The intercept of a line is the point where it crosses the y-axis, and it is calculated by setting x = 0 in the equation of the line. If two lines have the same intercept, then they are parallel.
To use the intercept method to prove lines parallel, follow these steps:
- Find the intercept of each line by setting x = 0 in the equation of the line.
- Compare the intercepts of the two lines. If the intercepts are equal, then the lines are parallel.
For example, consider the following two lines:
- Line 1: y = 2x + 1
- Line 2: y = 2x + 5
The intercept of Line 1 is 1, and the intercept of Line 2 is 5. Therefore, the two lines are not parallel.
Angle Relationships
Angle relationships can also be used to prove lines parallel. If two lines are cut by a transversal, then there are eight angles formed. The following angle relationships indicate that the lines are parallel:
- Alternate interior angles are congruent.
- Corresponding angles are congruent.
- Same-side interior angles are supplementary.
For example, consider the following diagram:

In this diagram, lines l and m are cut by transversal t. Angles 1 and 5 are alternate interior angles, and they are congruent. Therefore, lines l and m are parallel.
Additional Concepts
In addition to the methods of proving lines parallel discussed earlier, there are two other important concepts that can be used: transversals and midsegments.
Transversals, Practice 3-2 proving lines parallel
A transversal is a line that intersects two or more other lines. When a transversal intersects two parallel lines, it creates a number of angles. The properties of these angles can be used to prove that the lines are parallel.
There are three main types of transversals:
- Same-side interior angles: These are the angles that are on the same side of the transversal and on the inside of the parallel lines.
- Alternate interior angles: These are the angles that are on opposite sides of the transversal and on the inside of the parallel lines.
- Corresponding angles: These are the angles that are on opposite sides of the transversal and on the outside of the parallel lines.
The following theorems can be used to prove that lines are parallel based on the properties of transversals:
- If two lines are cut by a transversal and the same-side interior angles are congruent, then the lines are parallel.
- If two lines are cut by a transversal and the alternate interior angles are congruent, then the lines are parallel.
- If two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel.
Midsegments
A midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle. Midsegments have several important properties that can be used to prove that lines are parallel.
The following theorems can be used to prove that lines are parallel based on the properties of midsegments:
- The midsegment of a triangle is parallel to the third side of the triangle.
- The midsegment of a triangle divides the third side of the triangle into two congruent segments.
Applications of Parallel Lines
Parallel lines find widespread applications across various fields, including construction, architecture, and engineering, where their unique properties ensure structural integrity, aesthetic appeal, and efficient designs.
Construction
In construction, parallel lines play a crucial role in ensuring the stability and precision of structures. They are used:
- To align structural elements such as beams, columns, and walls, ensuring proper load distribution and preventing uneven settlement.
- To create level surfaces for flooring, ceilings, and countertops, ensuring a smooth and even finish.
- To establish reference points for measurements and layout, ensuring accuracy and consistency throughout the construction process.
Examples of construction projects that utilize parallel lines include:
- High-rise buildings with parallel walls and columns for structural support
- Bridges with parallel beams and girders for load-bearing capacity
- Roads and highways with parallel lanes for efficient traffic flow
Architecture
In architecture, parallel lines are employed to create visually appealing and functional designs. They are used:
- To create a sense of order, symmetry, and balance in building facades and interiors.
- To emphasize verticality or horizontality, depending on the orientation of the lines.
- To create optical illusions and depth perception through the use of parallel lines in perspective drawings.
Examples of architectural structures that incorporate parallel lines include:
- The Parthenon in Greece, with its parallel columns and pediments
- The Empire State Building in New York City, with its parallel setbacks
- The Sydney Opera House in Australia, with its parallel roof shells
Engineering
In engineering, parallel lines are essential for designing and constructing efficient and reliable systems. They are used:
- To create parallel electrical circuits, ensuring proper current flow and minimizing energy loss.
- To design parallel piping systems, ensuring optimal fluid flow and pressure distribution.
- To align mechanical components, such as gears and bearings, ensuring smooth operation and minimizing wear and tear.
Examples of engineering projects that rely on parallel lines include:
- Electrical power grids with parallel transmission lines for efficient power distribution
- Plumbing systems with parallel pipes for water supply and drainage
- Automotive engines with parallel cylinders for balanced power output
Helpful Answers
What is the definition of parallel lines?
Parallel lines are lines that never intersect, no matter how far they are extended.
How can I prove lines parallel using the slope method?
If two lines have the same slope, they are parallel.
What are some real-life examples of parallel lines?
Railroad tracks, the sides of a rectangle, and the edges of a ruler are all examples of parallel lines.